关于 Milthm 由单曲 Reality 计算单曲分数的函数

在一切开始之前，我们需要援引一下@mkzi-nya，也就是归梦在之前发布的研究成果。

给定分数 $s$ 和定数 $c$，则有关于 $s$ 和 $c$ 的函数

$$r(s,c)= \left\{ \begin{array}{lr} 0, & \quad c\in(-\infty,0.001) \\ c+1, & \quad s\in[1005000,1001000] \\ \dfrac{1.4}{e^{3.65\cdot(99.5-\frac{s}{10000})}+1}+c-0.4, & \quad s\in[995000,1005000) \\ \dfrac{e^{3.1\cdot\frac{s-980000}{15000}}-1}{e^{3.1}-1}\cdot0.8+c-0.5, & \quad s\in[980000,995000) \\ \dfrac{s}{280000}+c-4, & \quad s\in[700000,980000) \\ 0, & \quad s\in(-\infty,700000) \\ \end{array} \right.$$

可以看到，函数 $r$ 拥有两个变量。但是我们不妨想一下，对于同一首歌，它的定数是唯一确定的，所以对于同一首歌，我们不妨将变量 $c$ 看作一个常数。

那么当我们排除掉 $r(c)=0, \quad c\in(-\infty,0.001)$ 这个仅受变量 $c$ 影响的函数后，有关 $s$ 的函数

$$r(s)= \left\{ \begin{array}{lr} c+1, & \quad s\in[1005000,1001000] \\ \dfrac{1.4}{e^{3.65\cdot(99.5-\frac{s}{10000})}+1}+c-0.4, & \quad s\in[995000,1005000) \\ \dfrac{e^{3.1\cdot\frac{s-980000}{15000}}-1}{e^{3.1}-1}\cdot0.8+c-0.5, & \quad s\in[980000,995000) \\ \dfrac{s}{280000}+c-4, & \quad s\in[700000,980000) \\ 0, & \quad s\in(-\infty,700000) \\ \end{array} \right.$$

让我们看看它的函数图像：

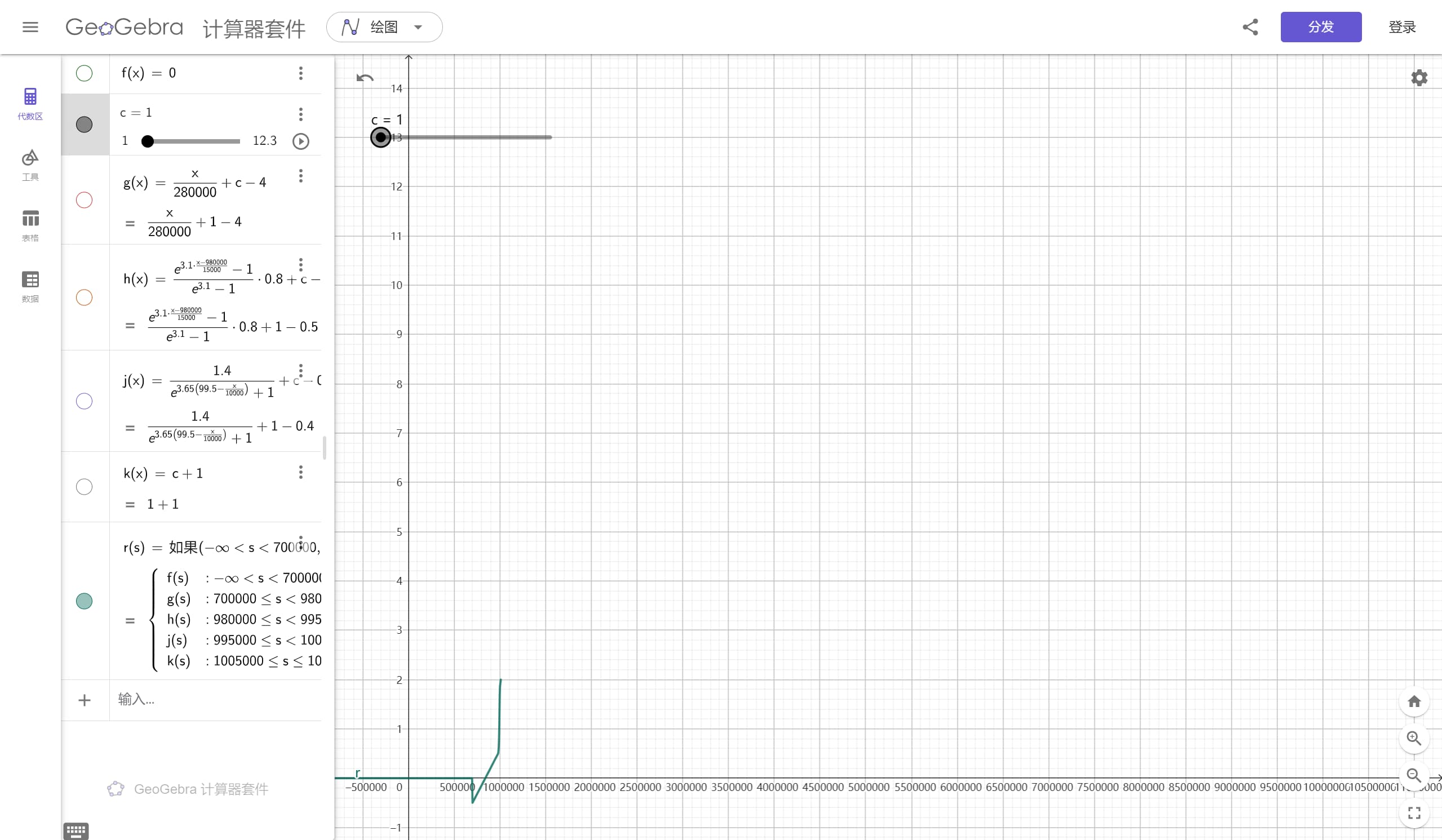
这是当它在目前定数最小值：1时的图像。函数的最小值约在 $x=700000$ 处取得（实际约在$x=700000.012373348$ 处取得）。

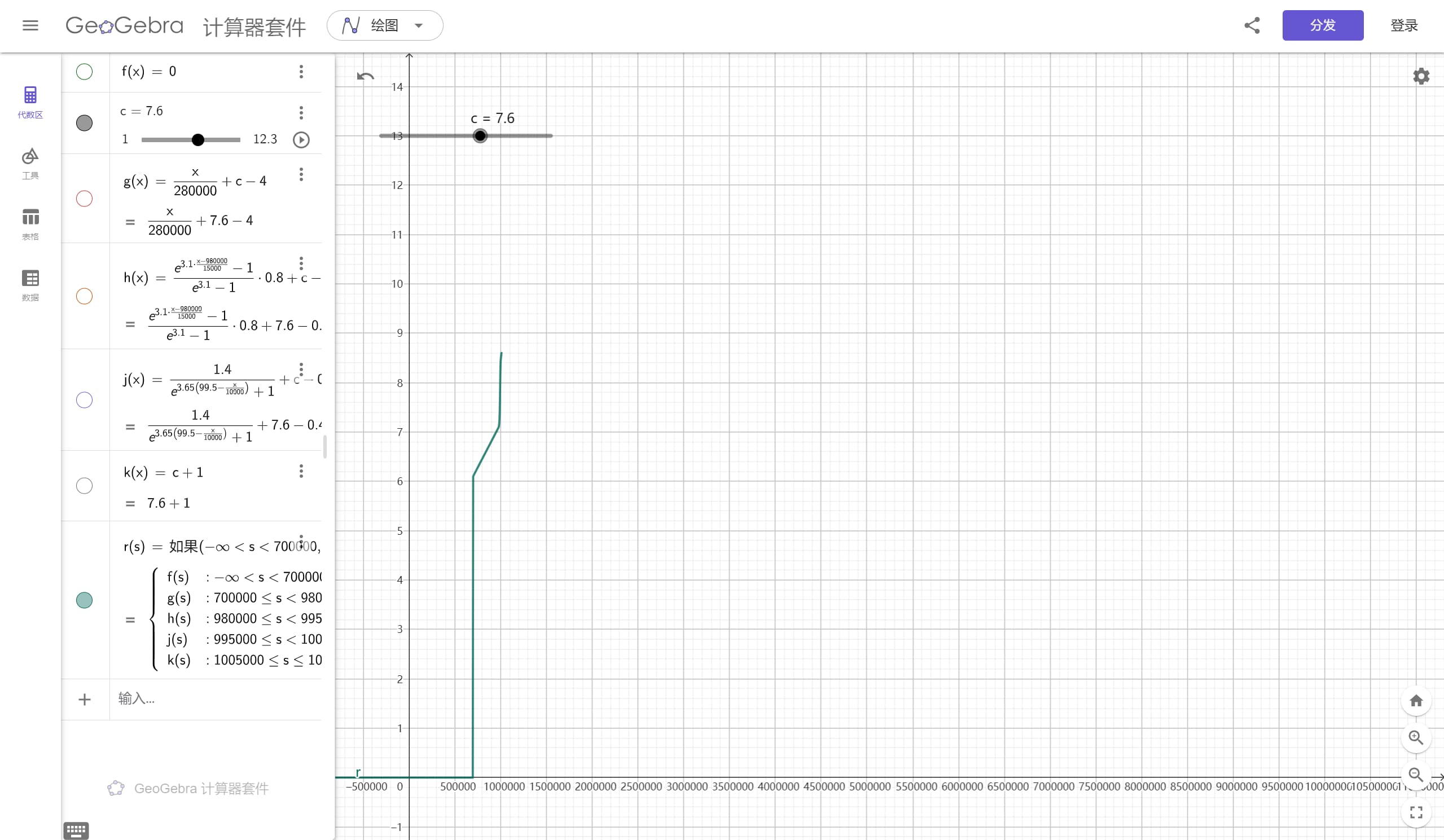
这是在极值之间任意取的一个数的函数图像。

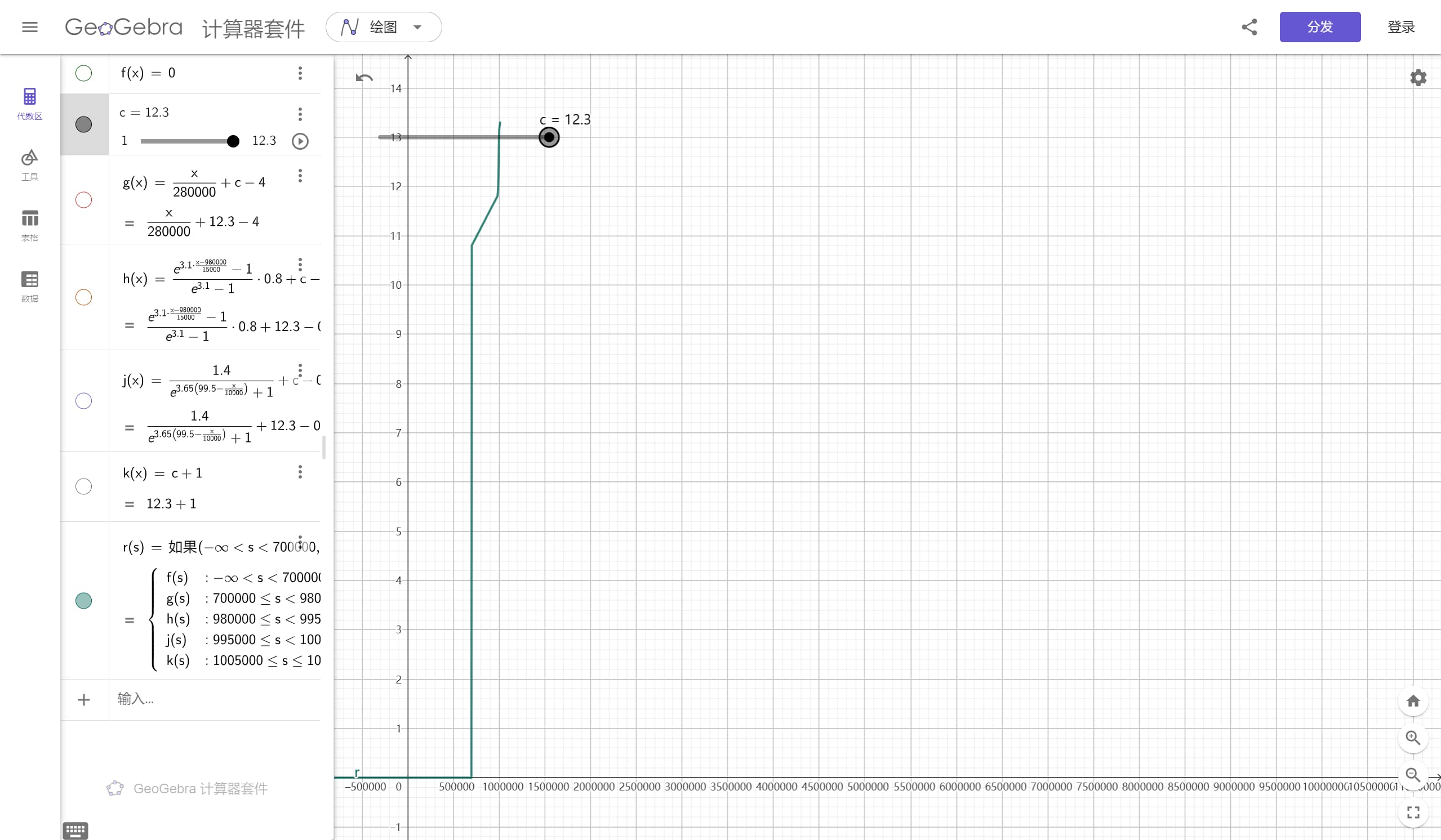
这是当它在目前定数最大值：12.3时的图像。

我们可以清楚地看到，函数 $r$ 在我们实际需要去计算单曲 Reality 的分数段 $s\in[700000,1010000]$ 内是单调递增的。

由于函数 $r$ 在 $s\in[700000,1010000]$ 内具有单调性，所以我们理应可以求得函数 $r$ 的反函数。

根据一些计算，我们可以得到函数 $r$ 的反函数

$$s(r)= \left\{ \begin{array}{lr} 10000\left(99.5-\dfrac{1}{3.65}\ln\left(\dfrac{c-r+1}{r-c+0.4}\right)\right), & \quad r\in\left[c+0.3,c+\dfrac{1.4}{e^{-3.65}+1}-0.4\right) \\ \dfrac{15000}{3.1}\ln\left(\dfrac{(r-c+0.5)(e^{3.1}-1)}{0.8}+1\right)+980000, & \quad r\in[c-0.5,c+0.3) \\ 280000(r-c+4), & \quad r\in[c-1.5,c-0.5) \\ \end{array} \right.$$

同时，由于函数 $r$ 两个极端情况取值为常数，所以有：

当 $r=c+1$ 时， $s\in[1050000,1010000]$ ；

当 $r=0$ 时， $s\in(-\infty,700000)$ 。

由此，我们就获得了由单曲 Reality 计算单曲分数的函数。

同时，由于单曲分数 $s$ 一定满足 $s\in\mathbb{N}$，所以实际计算过程中， 某一确定的单曲 Reality $r$ 对应的单曲分数 $s$ 可能是小数，这时可能需要做额外的处理。